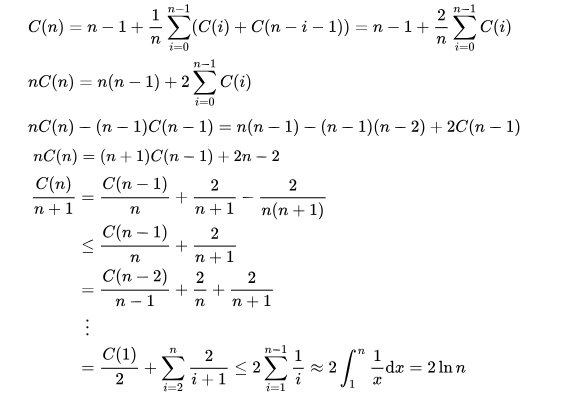QuickSort Algorithm

1 What’s QuickSort Algorithm?

Like MergeSort, QuickSort is one of the most efficient sorting algorithm based on the divide and conquer algorithm. It’s also a randomized algorithm. It picks an element as a pivot and partitions the given array around it such that: left side of the pivot contains all elements that are smaller than the pivot element, and right side of the pivot comprises all elements that are greater than the pivot element. Apply the partition process recursively to the left and right parts.

2 How QuickSort works?

There are three main steps:

1. Choose a pivot value;
2. Partition the given array around the pivot. Rearrange the array in such a way: all elements that are smaller than the pivot goes to the left side of the array, and all elements that are greater than the pivot goes to the right part of the array;
3. Sort both parts. Apply the partition process recursively to the left and right part;

3 Pseudo code

QuickSort(arr[], left, right) {

    pivot_index = partitions(arr[], left, right);
    QuickSort(arr, left, pivot_index - 1);
    QuickSort(arr, pivot_index + 1, right);

}

There are many different versions of quickSort that pick pivot in different ways.

1. Basic Quicksort: Always pick first(last) element as pivot.
2. Randomized Quicksort: Pick a random element as pivot.
3. Pivot Selection Using Median Finding.

/*
    choose the rightmost(leftmost) value as the pivot
*/
partitions(arr[], left, right) {
    if(left < right) {
        int i = left;
        int j = right - 1;
        while(i <= j){
            if(arr[i] >= arr[right]) {
                swap(arr[i], arr[j]);
                j--;    
                break;
            }
            i++;
       }
       swap(arr[right], arr[i]);
       return i;
    }
    return -1;
}

/*
    choose a randomized value as the pivot
*/
partitions(arr[], left, right) {
    int pivot_index = randomized(arr);
    swap(arr[pivot_index], arr[right]);
    if(left < right) {
        int i = left;
        int j = right - 1;
        while(i <= j){
            if(arr[i] >= arr[right]) {
                swap(arr[i], arr[j]);
                j--;    
                break;
            }
            i++;
       }
       swap(arr[right], arr[i]);
       return i;
    }
    return -1;
}

/*
    choose a median value as the pivot.
*/
partitions(arr[], left, right) {
    int pivot_index = linear_time_median_finding(arr);
    swap(arr[pivot_index], arr[right]);
    if(left < right) {
        int i = left;
        int j = right - 1;
        while(i <= j){
            if(arr[i] >= arr[right]) {
                swap(arr[i], arr[j]);
                j--;    
                break;
            }
            i++;
       }
       swap(arr[right], arr[i]);
       return i;
    }
    return -1;
}

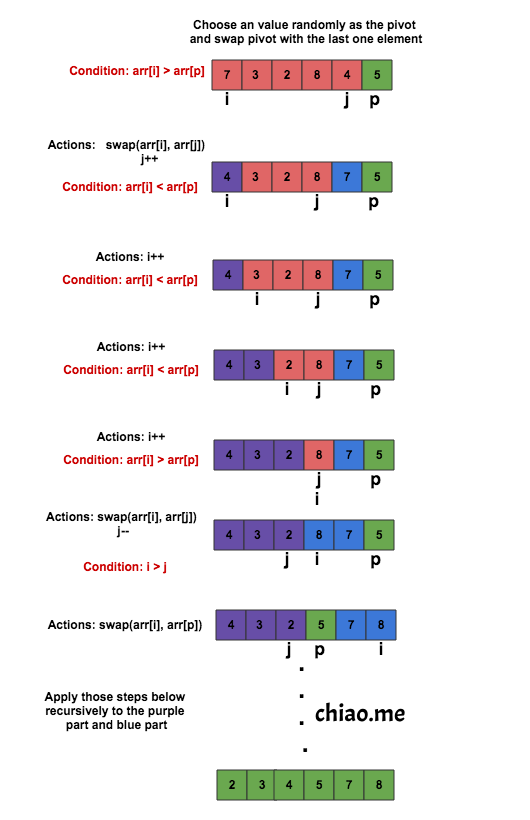
4 Example

What’s the meaning of i, j, p?

1) the values in [0,i) are less than the pivot;
2) the values in [i, j] need to be explored;
3) the values in [j, n-1] are greater or equal than the pivot;

5 Code Rush

Java Version

import java.util.Random;
import java.util.Arrays;
public class QuickSort {
    private Random ran;
    public QuickSort(Random ran) {
        this.ran = ran;
    }
    public void quickSort(int[] arr) {
        quickSortHelper(arr, 0, arr.length - 1);
        return;
    }
    public void quickSortHelper(int[] arr, int left, int right) {
        if(left < right) {
            int pivot = generateRandomNumber(left, right);
            swap(arr, pivot, right);
            int res = partitions(arr, left, right);
            quickSortHelper(arr, left, res - 1);
            quickSortHelper(arr, res + 1, right);
        }
        return;
    }
    public int partitions(int[] arr, int left, int right) {
        int i = left;   
        int j = right - 1;   
        int p = right;  
        while(i <= j) {    
            if(arr[i] > arr[p]) {
                swap(arr, i, j);
                j--;
                continue;
            }
            i++;
        }
        swap(arr, i, p);
        return i;
    }
    public void swap(int[] arr, int a, int b) {
        int tem = arr[a];
        arr[a] = arr[b];
        arr[b] = tem;
        return;
    }
    public int generateRandomNumber(int left, int right) {
        return this.ran.nextInt(right - left + 1) + left ;
    }

    public static void main(String[] args) {
        Random ran = new Random();
        QuickSort q = new QuickSort(ran);
        int[] arr = new int[]{3, 4, 1, 2, 10, 9, -10};
        System.out.println(Arrays.toString(arr));
        q.quickSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

6 Time & Space complexity

Time complexity:

The time complexity of QuickSort depends on if the partitions are balanced. The balanced partition is determined by the pivot. According to the algorithm, the time taken by QuickSort, in general, can be written as follows:

T(n) = T(k) + T(n - k - 1) + O(n);

The first two terms are for recursive calls, and the last one is for the partition process. K is the number which is smaller than the pivot. The time taken by QuickSort depends on the input array and partition strategy. Following are three cases.

1.Worst Case:

The worst case occurs when the partitions always pick the greatest and smallest element as a pivot. If we consider basic QuickSort where the last or first element is always picked as the pivot, the worst case will occur when is array is already sorted in increasing or decreasing order. Following is the expression for the worst case.

T(n) = T(0) + T(n - 1) + O(n);

The time complexity of above is O(n*n).

Best Case:

The best case occurs when the partition process always picks the middle element as the pivot. Following is an expression for the best case.

T(n) = 2T(n / 2) + O(n);

The time complexity of above is O(nlogn).

Average case:

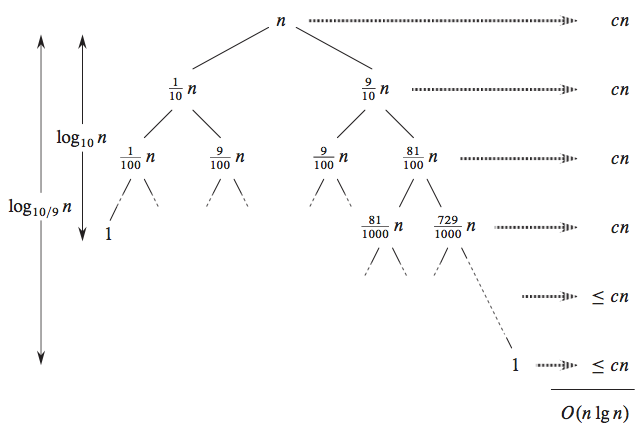
To do average case analysis, we need to consider all possible permutation of the array and calculate time taken by every permutation which doesn’t look easy. We can get the idea of the average case by considering the fact when partition puts O(n/10) element in one set and O(9n/10) aspects in other sets. There are a few possibilities for this case to happen. Following is the expression for this case.

T(n) = T(n/9) + T(10/n) + O(n);

Let’s analyze this situation:

From the picture, we can see that the time complexity is also O(nlogn). This is an approximate analysis. Now, we consider all possible permutation.

Solving the recurrence gives C(n) = 2nlnn ≈ 1.39nlogn.

Therefore, the solution is O(nlogn).

Space complexity:

About the space complexity, we quote Wikipedia’s explanation, which is detailed.

The space used by quicksort depends on the version used. The in-place version of quicksort has a space complexity of O(log n), even in the worst case, when it is carefully implemented using the following strategies: 1).in-place partitioning is used. This unstable partition requires O(1) space. 2).After partitioning, the partition with the fewest elements is (recursively) sorted first, requiring at most O(log n) space. Then the other partition is sorted using tail recursion or iteration, which doesn’t add to the call stack. This idea, as discussed above, was described by R. Sedgewick, and keeps the stack depth bounded by O(log n).

7 Why is QuickSort preferred over MergeSort for Arrays?

1.QickSort has in-place sort that requires O(logn) space complexity(used for call stack), whereas MergeSort requires O(n) space, which may be quite expensive. Allocating and deallocating the extra space used for MergeSort increases the running time of the algorithm. Comparing average complexity, we find that both types of sorts have O(NlogN) average complexity, but the constants differ. For arrays, MergeSort loses due to the use of extra O(N) storage space.

2.QuickSort is a cache friendly sorting algorithm as it has good locality of reference when used for arrays. quicksort changes the array in-place - in the array it is working on [unlike merge sort, for instance - which creates a different array for it]. Thus, it applies the principle of locality of reference.

Cache benefits from multiple accesses to the same place in the memory, since only the first access needs to be actually taken from the memory - the rest of the accesses are taken from the cache, which is much faster the access to memory.

Merge sort for instance - needs much more memory [RAM] accesses - since every accessory array you create - is accessing the RAM again.

Trees are even worse - since 2 sequential accesses in a tree are not likely to be close to each other. [Cache is filled in blocks, so for sequential accesses - only the first byte in the block is a “miss” and the others are a “hit”].

3.QuickSort is also tail recursive, therefore tail call optimization is done.

8 Variants

1. Sorting Single(double) Linked List;
2. Sorting string.
3. Implementing QuickSort Iteratively.

9 Interview Skills Sharing

1. Tips to Get the Most Out of Career Fairs

References

1.https://en.wikipedia.org/wiki/Quicksort#Space_complexity 2.https://www.geeksforgeeks.org/quick-sort/ 3.https://www.geeksforgeeks.org/analysis-of-algorithms-set-2-asymptotic-analysis/ 4.http://interactivepython.org/runestone/static/pythonds/SortSearch/TheQuickSort.html 5.https://www.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/overview-of-quicksort

• Previous
  MergeSort Algorithm
• Next
  Recursion