1 What’s Recursion?
Recursion in computer science is a method of solving the problem where the solution depends on solutions to smaller instances of the same problem.
Sometimes a problem is too difficult or too complicated to solve because it’s too big. If the problem can be broken down into smaller versions of itself, it may be able to find a way to address one of these smaller versions and then be able to build up to a solution to the entire problem. That is is the idea behind the recursion. Recursive algorithms break down a problem into smaller pieces which you already know the answer to and can solve by applying the same algorithm to each section, and then combining the results. Recursive algorithms can be implemented by the process in which a function calls itself directly or indirectly until the smallest case is reached.

2 What the principle of Recursion?
A recursive function in recursion algorithm consists of two parts:
- Base Case: a recursive function has one or more base cases that breaks the chain of recursion;
- Recursive Rule: the job of recursive rule can be seen as breaking down complex problem into simpler ones until the base case is reached;
3 Types of recursion
1). Single recursion and multiple recursion
Recursion that only contains a single self-reference is known as Single recursion, while recursion that contains multiple self-references is known as Multiple recursion. Single recursion is often more efficient than multiple recursion, can generally be replaced by an iterative program, which runs in linear time and requiring constant time. Multiple recursion, by contrast, may require exponential time and space, and is more fundamentally recursive, not be able to replaced by iteration without an explicit stack. Multiple recursion can be sometimes converted to single recursion.
2). Structural recursion versus generative recursion
The key difference between structural recursion and generative recursion is where a recursive procedure gets data that it works on and how it processes that data. Specifically, for structural recursion, a recursive call is made on a subset of original input data. Whereas for generative recursion, a recursive call is made on data that is constructed or calculated from the original input data.
The term “structural recursion” comes from the fact that these structures (list, BST, natural numbers, Fibonacci number, Factorial number, etc.) can be defined recursively.
Structural recursion includes nearly all tree traversals, including XML processing, binary tree creation, and search, etc. By considering the algebraic structure of the natural numbers (that is, a natural number is either zero or the successor of a natural number), functions such as factorial may also be regarded as structural recursion.
Many well-known recursive algorithms generate an entirely new piece of data from the given data and recur on it. HtDP (How To Design Programs) refers to this kind as generative recursion. Examples of generative recursion include gcd, quicksort, binary search, mergesort, Newton’s method, fractals, and adaptive integration.
4 Recursive data structure
An important application of recursion in computer science is in defining dynamic data structures such as lists and trees. A data structure that is partially composed of smaller or simpler instances of the same data structure. For instance, a tree is composed of smaller trees (subtrees) and leaf nodes, and a list may have other lists as elements.
Recursive algorithms are particularly appropriate when the underlying problems or the data to be treated are defined in recursive terms.
1). Linked list
A linked list is either:
- the empty list, represented by None, or
- a node contains a cargo object and a reference to linked list
2). Tree
A tree is either:
- empty
- a vertex r (the root of T) and a set of trees (the subtrees of T) whose roots are the children of r.
5 Recursive programs
1). Fibonacci sequence
I. Recursive formula
Base Case:
$$f(0) = 0; f(1) = 1;$$
Recursive rules:
$$f(n) = f(n - 1) + f(n - 2);$$
public class Fibonacci {
public int fib(int n) {
if(n == 0) {
return 0;
} else if(n == 1) {
return 1;
}else {
return fib(n - 1) + fib(n - 2);
}
}
public static void main(String[] args) {
Fibonacci f = new Fibonacci();
System.out.println(f.fib(5));
}
}
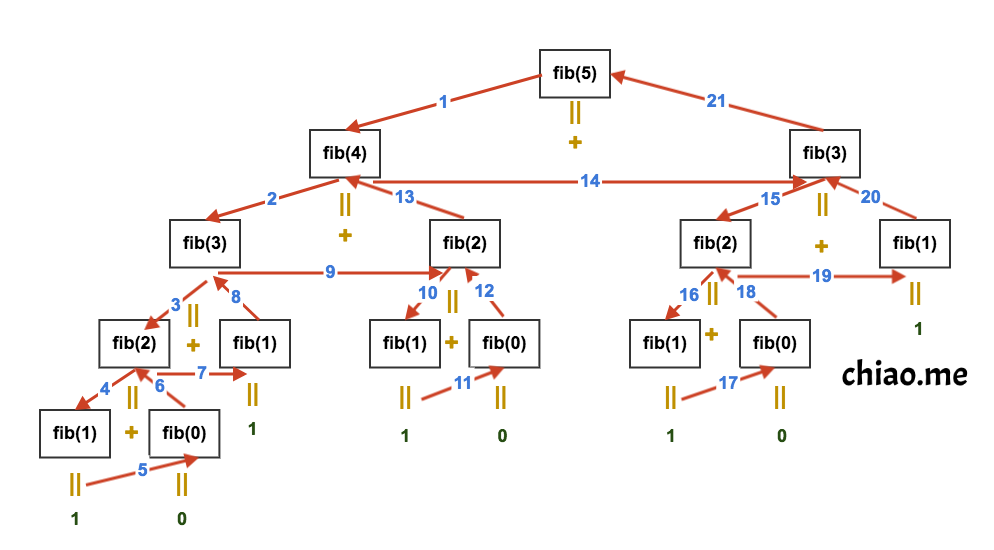
II. Program execution flow
The following illustrates the actual execution flow for this recursive call based on the original input.
fib(5)
fib(4)
fib(3)
fib(2)
fib(1)
fib(0)
fib(1)
fib(2)
fib(3)
Values at the same level of indentation are summed to produce the result for the previous level of indentation.
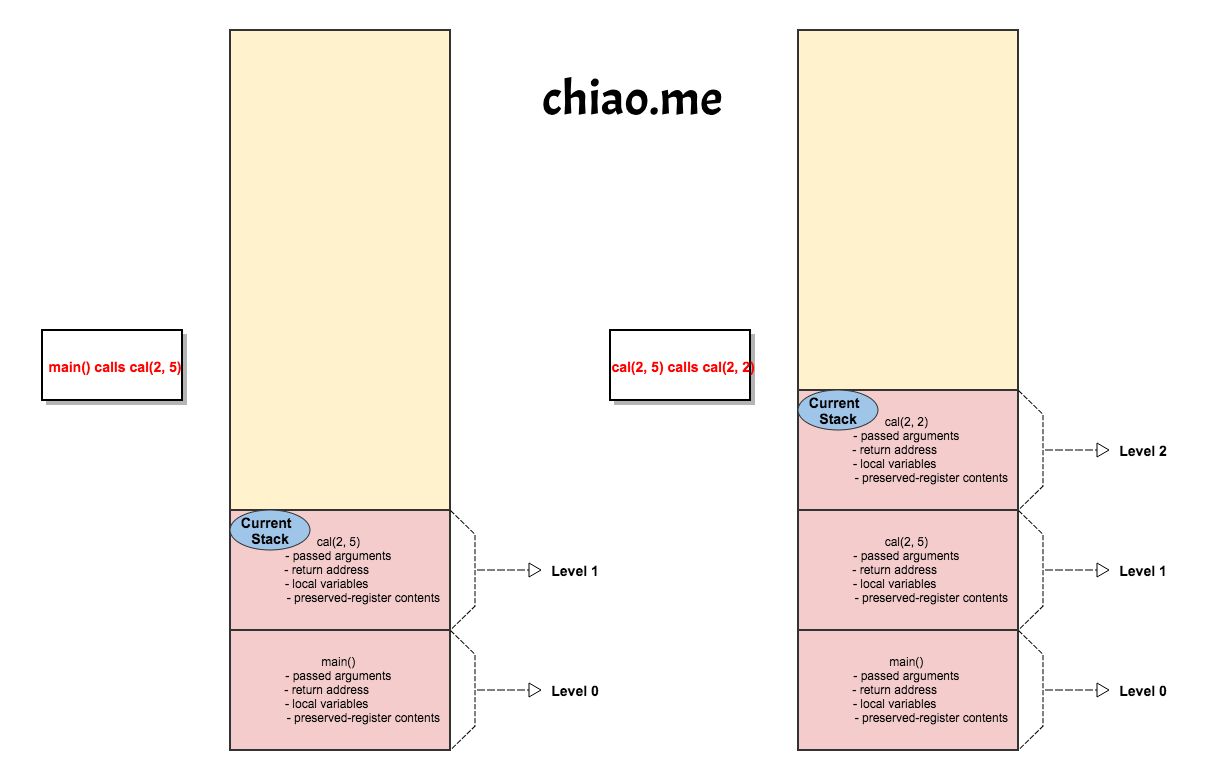
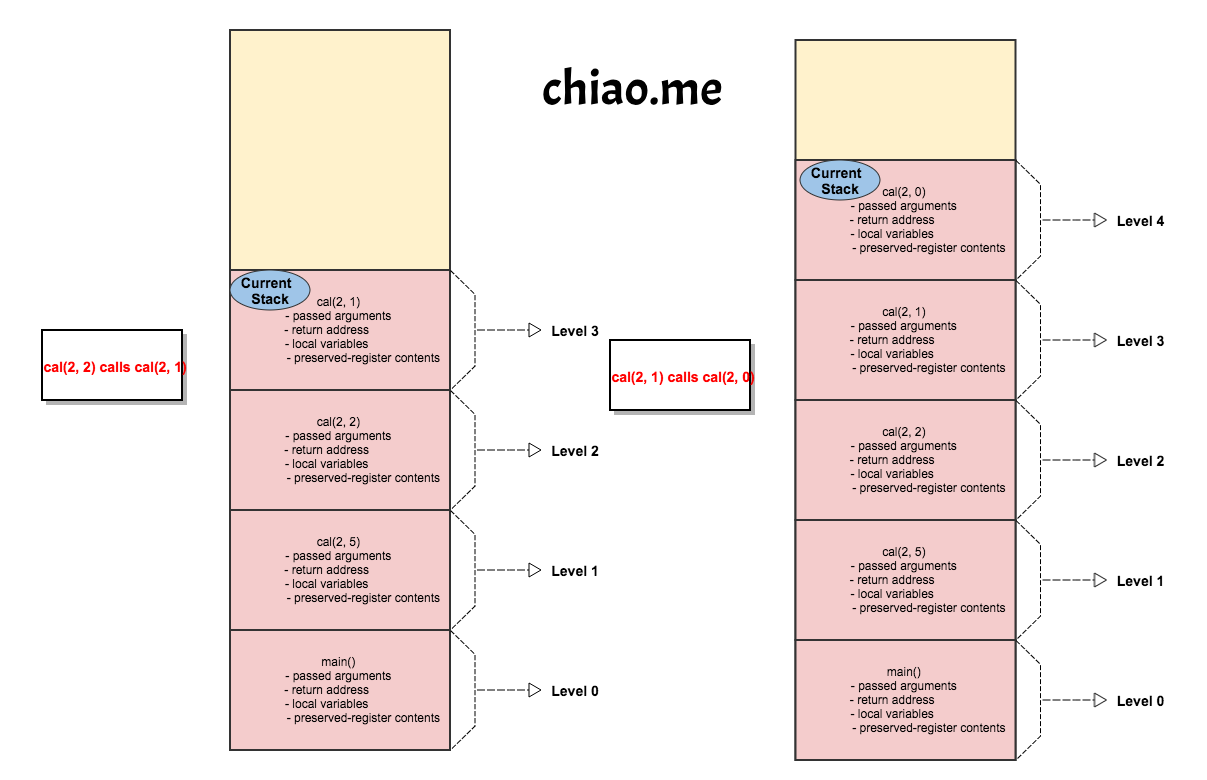
III. Call stack
Each called function (“callee”) has a stack frame containing the following parts:
- passed arguments
- return address
- local variables
- preserved-register contents
You can click here to see big pictures.
IV Time complexity
Generally speaking, there are two methods of calculating time complexity for recursive program. One is to draw recursive tree, which is a intuitive way to show running times. The other is to calculate time complexity through master theory.
The time complexity is total number of all nodes:
\[O(n) = 1 + 2 + 4 + 8 +....+ 2^n\]We can see the number of the last level as the sum of nodes in previous levels. Therefore, the time complexity is \(O(2^n)\).
- Master Theory
We can write the recursive expression:
\[T(n) = T(n - 1) + T(n - 2) + O(1)\]Apply the master theory to this expression:
\[T(n) = O(1.6180^n)\]V Space complexity
The best way to calculate the space complexity of recursion is (the number of stack frames) * (space per stack frame) There is one thing we should notice that ‘the number of stack frames’ refers to the maximum number of stack frames coexisting at the same time. For this case the space complexity is equal to
$$O(n) = n \times O(1) = O(n)$$
2). Calculate \(f(a,b) = a^b\)
We assume that a and b are integers, and we neglect the corner case that a = 0, b < 0.
I. Recursive formula
Base Case:
When b = 0:
$$f(a, b) = 1$$
Recursive Case:
1) When b != 0 and b / 2 = 0:
$$f(a, b) = f(a, \frac{b}{2}) \times f(a, \frac{b}{2})$$
2) When b != 0 and b / 2 != 0:
$$f(a, b) = f(a, \frac{b}{2}) \times f(a, \frac{b}{2}) \times a $$
public class Cal {
public int cal(int a, int b) {
if(b == 0) {
return 1;
}else {
int half = b / 2;
int half_value = cal(a, half);
if(b % 2 == 0) {
return half_value * half_value;
}else {
return half_value * half_value * a;
}
}
}
public static void main(String[] args) {
Cal c = new Cal();
System.out.println(c.cal(2, 5));
}
}
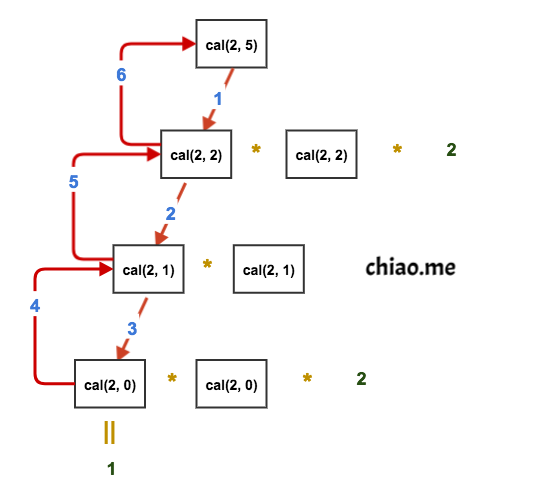
II. Program execution flow
The following illustrates the actual execution flow for this recursive call.
cal(2, 5)
cal(2, 2)
cal(2, 1)
cal(2, 0)
III. Program execution flow
The following diagrams display a series of stack frames when the program execute.
IV Recursive tree
V Time & Space complexity
The time complexity is equal to the total number of nodes, which is O(logn). The space complexity is euqal to (the number of stack frames) * (space per stack frame), which is O(logn).
3). Binary Search
Binary search is the search algorithm used to find the position of the target value in a list with the certain logic. This list can be a sorted array or a string with a certain rule. All in all, this list should be equipped with some rules.
I Classical problem
Check if the target value is in a sorted array.
public class BinarySearch{
public int binarySearch(int target, int[] arr) {
int arrLength = arr.length;
return helper(target, arr, 0, arrLength - 1);
}
public int helper(int target, int[] arr, int left, int right) {
if(left <= right) {
int mid = (right + left) / 2;
if (arr[mid] == target) {
return mid;
}else if(arr[mid] > target){
return helper(target, arr, left, mid - 1);
}else {
return helper(target, arr, mid + 1, right);
}
}
return -1;
}
public static void main(String[] args) {
BinarySearch b = new BinarySearch();
int[] arr = new int[]{1, 2, 3, 5, 6, 9};
int res = b.binarySearch(5, arr);
System.out.println(res);
}
}
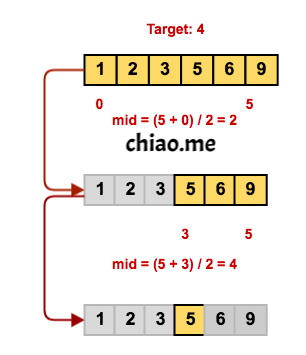
I Recursive tree
II Time & Space complexity
The time complexity is equal to the total number of nodes, which is log(n). The space complexity is O(1) because this recursive procedure is tail recursion.
References
- https://en.wikipedia.org/wiki/Recursion_(computer_science)#Recursive_procedures
- https://www.geeksforgeeks.org/recursion/
- https://www.geeksforgeeks.org/tail-call-elimination/
- http://www.cs.kent.edu/~javed/class-ALG06F/webbook/ALG00S-L03b.pdf
- http://www.sparknotes.com/cs/recursion/whatisrecursion/section1/
- https://stackoverflow.com/questions/14268749/how-does-structural-recursion-differ-from-generative-recursion
- https://pdfs.semanticscholar.org/presentation/d913/02528df5f43f6ab8fe939326480b556b4490.pdf
- https://discuss.codecademy.com/t/recursive-function-calls/65109/3
- https://stackoverflow.com/questions/8845154/how-does-the-fibonacci-recursive-function-work/8845269
- https://www.geeksforgeeks.org/time-complexity-recursive-fibonacci-program/
- https://practice.geeksforgeeks.org/problems/space-complexity-of-fibonacci-recursion
- *http://www.cs.cornell.edu/info/courses/spring-98/cs211/lecturenotes/07-recursion.pdf