algorithms data structure

Stack

An abstract data type and a linear data structure

Posted by Zhao Chang on September 26, 2018

1 What’s the Stack?

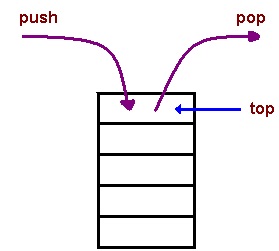
A stack is an abstract data type and a linear data structure that serves a collection of elements, with two principal operations:

  • push, which adds an element to the collection;
  • pop, which removes the most recently added element that was not yet removed.

This feature makes it LIFO data structure, which stands for Last-In-First-Out.

2 Implementation

A stack can be easily implemented by either through an Array or a linked list. What identifies the data structure as a stack is not the implementation but the interface. The user is only allowed to pop and push items onto the array or linked list. One important thing when the stack implemented by an array or linked list is to store the top position that is either the index of the rightmost value or the tail of the linked list.

3 Applications of stacks

If you are required to implement an algorithm by stack, you should consider using more than one stacks.

1). Implement a queue using two stacks

I Solution:
  • One stack is for pushing element;
  • One stack is for popping element;
  • when the stack used to pop is empty, all elements in the stack used to push need to be moved to the pop stack.
import java.util.Stack;
import java.lang.Integer;
public class IQueue{
    private Stack<Integer> pushStack = new Stack<Integer>();
    private Stack<Integer> popStack = new Stack<Integer>();
    public void push(int val) {
        pushStack.push(val);
    }

    public int pop() {
        if(popStack.empty()) {
            while(!pushStack.empty()) {
                popStack.push(pushStack.pop());
            }
        }
        return popStack.pop();
    }
    public static void main(String[] args) {
        IQueue iq = new IQueue();
        for (int i = 0; i < 1000; i++) {
            iq.push(i);
        }
        for (int i = 0; i < 100; i++) {
            System.out.println(iq.pop());
        }
        for (int i = 0; i < 1000; i++) {
            iq.push(i);
        }
        for (int i = 0; i < 1900; i++) {
            System.out.println(iq.pop());
        }

    }
}
II Time complexity

We can find that the operation of push always takes constant time, and the operation of pop takes constant time. However, few operations of pop don’t take constant time, which occurs when the stack used to pop is empty. The best way to calculate time complexity is to analyze amortized time.

Let’s assume that there are n elements need to be popped in the new queue, t is the number of elements lie in popStack, n - t is the number of element lie in pushStack.

\[O(n) = \frac{( 2 \times (n - t) + n )}{n} = \frac{(3 - 2t )}{n} <= 3 = O(1)\]

2) Design and implement a stack that supports getMin() in O(1) time

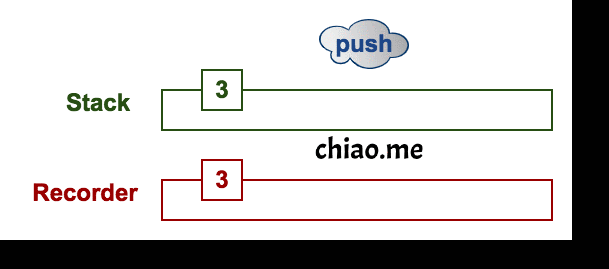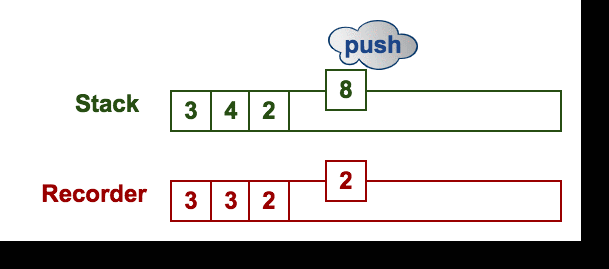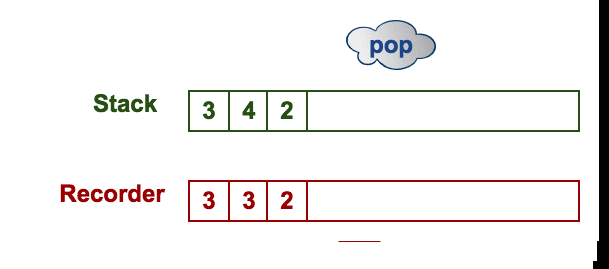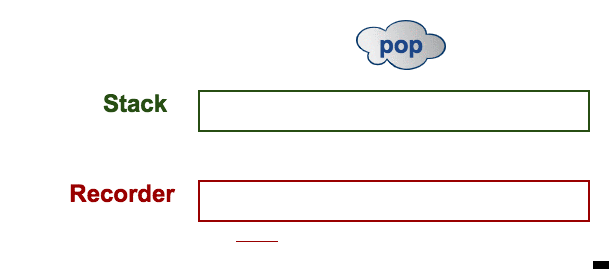
One easy solution is that we can record the min of every status for the stack. We need to update the min after every pop or push operation. Therefore, using another stack is a better way to keep the same pace with the original stack.

Solution:

  • One stack is for operating elements (push and pop)
  • The other stack is for recording the min and keeping the same pace with the original stack.
import java.util.Stack;
import java.lang.Integer;
public class Solution {
    private Stack<Integer> store = new Stack<>();
    private Stack<Integer> recorder = new Stack<>();
    private int globalMin = Integer.MAX_VALUE;

    public void push(int val) {
        if (store.empty() || globalMin > val) {
            store.push(val);
            recorder.push(val);
            globalMin = val;
        } else {
            store.push(val);
            recorder.push(globalMin);
        }
    }

    public int pop() {
        recorder.pop();
        return store.pop();
    }

    public int getMin() {
        return recorder.peek();
    }

    public static void main(String[] args) {
        Solution s = new Solution();
        s.push(3);
        s.push(5);
        s.push(1);
        s.push(9);
        s.push(10);
        System.out.println(s.getMin());
        s.pop();
        s.pop();
        s.pop();
        s.pop();
        System.out.println(s.getMin());
    }
}

3) Design and implement a stack that supports getMin() in O(1) time and O(1) extra space

This is a challenging problem. It is easy to employ O(n) space to keep track of the min value for each operation. Are there other solutions to achieve the same goal with constant extra space? The answer is yes. Although it’s not possible to use constant variables to record all changes, we can achieve the same result with the help of an already existing stack.

I. Solution:
  • Use global variable min to record the global minimum value;
  • when push element, compare the element to min;
    • if min <= element, insert the element into the stack
    • if min > element, insert newVal ( 2 * element - min) into the stack and let min be equal to the element
  • when pop element, compare the element to min
    • if min <= element, pop element directly
    • if min > element, return min and let min be equal to (2 * min - newVal)

II. Why does this method work?

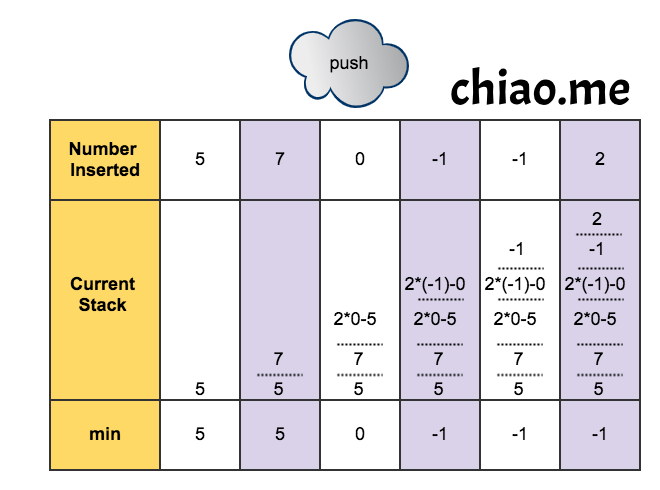
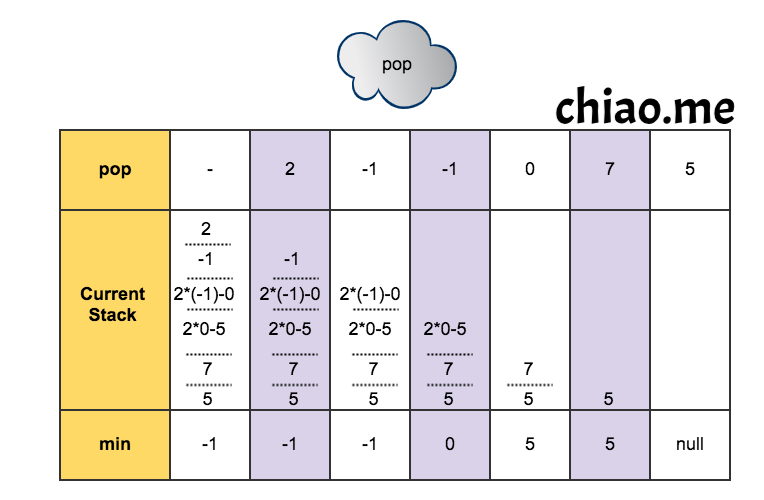
The key thing is to record the previous minimum value in the current operation. The reason is that we need to decide if the minimum value should be updated when the new element is inserted. There are two situations. One is the element is bigger than the minimum value. The global min has no change. The other is the element is equal to the minimum value. The global min should be changed to the previous minimum value. Therefore, one flag is required to display the global min should be updated. In the solution, 2 * element - min serves as the flag that is compared to the current min.

If 2 * element - min is less than the current min, it suggests that the original element should be the minimum value. Therefore, 2 * element - min has two purposes: 1) encode the previous minimum value. 2) mark the change of min.

Why is 2 * element - min right?

Let x be the value of element
    when x >= min, we just put x,
    when x < min, we can get:
        x - min < 0   ==>   x + x - min < x; This will ensure that 2x - preMin is always smaller that currMin.

import java.util.Stack;
import java.lang.Integer;
public class Solution{
    private Stack<Integer> store = new Stack<Integer>();
    private int globalMin = Integer.MIN_VALUE;

    public int getMin() {
        if(store.empty()) {
            return Integer.MIN_VALUE;
        }else {
            return globalMin;
        }
    }

    public void push(int val) {
        if(store.empty()) {
            store.push(val);
            globalMin = val;
        }
        if(val >= globalMin) {
            store.push(val);
        }else {
            int tem = 2 * val - globalMin;
            store.push(tem);
            globalMin = val;
        }
    }

    public int pop() {
        if(store.empty()) {
            return Integer.MIN_VALUE;
        }
        int popTem = store.pop();
        if(popTem >= globalMin) {
            return popTem;
        }else {
            int tem = globalMin;
            globalMin = 2 * globalMin - popTem;
            return tem;
        }
    }
    public static void main(String[] args) {
        Solution s = new Solution();
        s.push(-4);
        s.push(3);
        s.push(-41);
        s.push(1);
        s.push(3);
        s.push(2);
        s.push(-5);
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.getMin());
    }
}
III. Variant: Implement a stack that supports getMax() in O(1) time and constant extra space.
import java.util.Stack;
import java.lang.Integer;
public class Solution{
    private Stack<Integer> store = new Stack<>();
    private int globalMax = Integer.MAX_VALUE;
    public void push(int val) {
        if(store.empty()) {
            store.push(val);
            globalMax = val;
        }else {
            if(val <= globalMax) {
                store.push(val);
            }else {
                int tem = 2 * val - globalMax;
                store.push(tem);
                globalMax = val;
            }
        }
    }
    public int pop() {
        if(store.empty()) {
            return Integer.MAX_VALUE;
        }
        int popTem = store.pop();
        if(popTem <= globalMax) {
            return popTem;
        }else {
            int tem = globalMax;
            globalMax = 2 * globalMax - popTem;
            return tem;
        }
    }
    public int getMax() {
        if(store.empty()){
            return Integer.MAX_VALUE;
        }
        return globalMax;
    }

    public static void main(String[] args) {
        Solution s = new Solution();
        s.push(-4);
        s.push(3);
        s.push(-41);
        s.push(1);
        s.push(3);
        s.push(2);
        s.push(-5);
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.pop());
        System.out.println(s.getMax());
    }

}

4) Sort a stack using a temporary stack

I. Solution:
  • While stackOne is not empty do this:
    • Pop an element from stackOne and call it tem;
    • While stackTwo is not empty and the top of the stackTwo is greater than tem;
      • Pop from stackTwo and push it to stackOne;
    • Pop from stackTwo and push it to stackOne;
  • The sorted number are in stackTwo.
import java.util.Stack;
import java.lang.Integer;
public class Solution{
    private Stack<Integer> stackTwo = new Stack<>();
    public Stack<Integer> sortStack(Stack<Integer> stackOne) {
        while(!stackOne.empty()) {
            int tem = stackOne.pop();
            while(!stackTwo.empty() && stackTwo.peek() > tem) {
                stackOne.push(stackTwo.pop());
            }
            stackTwo.push(tem);
        }
        return stackTwo;
    }

    public static void main(String[] args) {
        Solution s = new Solution();
        Stack<Integer> stackOne = new Stack<>();
        stackOne.push(100);
        stackOne.push(10);
        stackOne.push(-1);
        stackOne.push(-1);
        stackOne.push(2);
        stackOne = s.sortStack(stackOne);
        while(!stackOne.empty()) {
            System.out.println(stackOne.pop());
        }
    }
}

5). Largest Rectangle in Histogram (leetcode 84)

6). Evaluate Reverse Polish Notation

Reverse Polish notation (RPN), also known as Polish postfix notation or simply postfix notation, is a mathematical notation in which operators follow their operands, in contrast to Polish notation (PN), in which operators precede their operands.

I. Solution:
  • Push operands to the stack until operand comes up;
  • Pop first two operands from the stack, and do operation.
class Solution {
    	public  int evalRPN(String[] tokens) {
            int len = tokens.length;
            Stack<Integer> store = new Stack<>();
            for(String token : tokens) {
                if(!token.equals("+") && !token.equals("-") && !token.equals("*") && !token.equals("/") ) {
                    store.push(Integer.parseInt(token));
                }else {
                    int b = store.pop();
                    int a = store.pop();
                    if (token.equals("+")) store.push(a + b);
                    if (token.equals("-")) store.push(a - b);
                    if (token.equals("*")) store.push(a * b);
                    if (token.equals("/")) store.push(a / b);
                }
            }
            return store.peek();
	}
}

References

  1. https://en.wikipedia.org/wiki/Stack_(abstract_data_type)
  2. https://www.geeksforgeeks.org/design-and-implement-special-stack-data-structure/
  3. https://www.geeksforgeeks.org/design-a-stack-that-supports-getmin-in-o1-time-and-o1-extra-space/
  4. https://www.geeksforgeeks.org/analysis-algorithm-set-5-amortized-analysis-introduction/
  5. https://www.geeksforgeeks.org/sort-stack-using-temporary-stack/
  6. https://leetcode.com/problems/evaluate-reverse-polish-notation/description/
FEATURED TAGS
talks Django Python Nginx statistics system visualization map visual analysis system design tools algorithms mergesort sort quicksort recursion Binary Search data structure
FRIENDS